

2.1. Тензор II валентности. Основные определения
Понятие о тензоре II валентности
Рассмотрим простейший случай, когда возникает потребность в тензоре. Закон Гука
F = - k Dx связывает две векторные величины–силу и растяжение/сжатие Dx под действием этой силы и в направлении силы, если речь идет, например, о растяжении свободно подвешенной пружины или сжатии пружины в направлении ее оси.Пусть некоторое тело закреплено в условиях невесомости на двух одинаковых пружинных растяжках
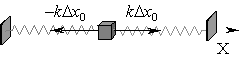
Под действием силы
F, направленной вдоль оси X, тело сместится вправо на Dx в новое положение равновесия,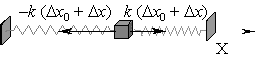
при котором
| <–k (Dx0 + Dx) + k(Dx0 – Dx) + F = 0, > | (1) |
или
F
= 2k Dx.Пусть теперь это же тело закреплено на пружинных растяжках так, как показано на следующем рисунке: каждая пара пружин, имеющая свой коэффициент упругости, параллельна какой-либо из координатных осей.
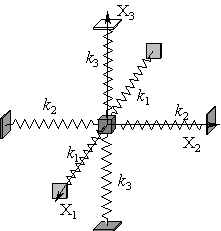
Если внешняя сила F = (F1,0,0) действует вдоль оси X1, то в новом положении равновесия она снова, как и в выражении (1), уравновешивается суммой сил упругости пружин с коэффициентами жесткости k1. Тело окажется смещенным на Dx1 вдоль оси X1, причем
| F1 = 2k1 Dx1. | (2) |
Предполагаем при этом, что сила достаточно мала, так что при смещении тела вдоль оси
X1 растяжения пружин, ориентированных вдоль других осей, практически не происходит.Аналогичные соотношения можно записать для случаев, когда сила действует в направлении осей
X2, X3:| F2 = 2k2 Dx2; F3 =2k3 Dx3. | (3) |
Если же сила имеет произвольное направление, ее можно разложить на три составляющие:
F = (F1,F2,F3), и для каждой составляющей записать соотношения вида (2), (3). Сила окажется связанной со смещением соотношением| F = e1 k1 Dx1 + e2 k2 Dx2 + e3 k3 Dx3. | (4) |
Отсюда видно, что, во-первых, вектор смещения тела не параллелен вектору внешней силы, если коэффициенты жесткости пружин различны. Во-вторых, если одновременно нужно рассматривать другое аналогично закрепленное тело с другой ориентацией пружин, вектор силы того тела в данной системе координат уже не будет связан с вектором смещения столь простой формулой, как (4). Чтобы установить связь между вектором силы и смещением тела в произвольно ориентированной системе координат, перепишем соотношение (4) в ином виде:
| F = e1 k11 Dx1 + e2 k22 Dx2 + e3 k33 Dx3 = ei kik Dxk, | (5) |
где в данной системе координат
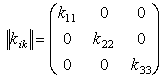
| (6) |
При повороте координатной системы компоненты векторов
F и Dr преобразуются по формулам (1.48)–(1.50). В новой системе координат компоненты вектора силы запишутся, согласно формуле (1.48), в виде Fj¢ = a j¢ i Fi. Выражая компоненты вектора силы в исходной системе координат посредством соотношения (5), а вектора перемещения посредством соотношения (1.49) Dxk = al¢ k Dxl¢ , получимFj¢ =
a j¢ i Fi = a j¢ i kik Dxk = a j¢ i kik al¢ k Dxl¢ = a j¢ i al¢ k kik Dxl¢ .Последнюю формулу представим в инвариантном, т. е. не зависящем от системы координат, виде:
| Fj¢ = kj¢ l¢ Dxl¢ , | (7) |
где
kj¢ l¢
= a j¢ i a l¢ k kik.Таким образом, в произвольной системе координат параметры подвески тела на пружинах определяются девятью величинами
kik, которые могут быть выражены (в данном конкретном случае) через три числа k11, k22, k33, связанных с определенной координатной системой.Если совокупность девяти величинTik при переходе от одной прямолинейной прямоугольной системы координат к другой преобразуется по формулам
| Tj¢ l¢ = a j¢ i al¢ k Tik, где a j¢ i = (ej¢ ei), | (8) |
совокупность этих девяти величинTik определяет геометрический объект, называемый тензором второй валентности (второго ранга) в трехмерном пространстве.
Величины
Tik называют компонентами тензора. Тензор второй валентности с компонентами Tik может быть представлен квадратной матрицей
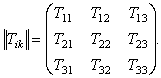
| (9) |
Кроме матричной записи тензора в форме (9), применяют еще следующие способы: (
Tik), T. Как и в случае квадратной матрицы, компоненты тензора T11, T22, T33 называются диагональными.Обратные соотношения, связывающие компоненты тензора в нештрихованной системе координат с компонентами штрихованной, имеют вид
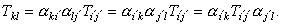 | (10) |
При использовании той же совокупности коэффициентов a j¢ i , что и в соотношениях (8), суммирование выполняется, в отличие от формул (8), по первым индексам.
Если
Tij представляют собой компоненты тензора T второй валентности, то совокупность девяти величин Qij = Tji также является тензором второй валентности. Действительно,a
j¢ i a l¢ k Qik = a j¢ i a l¢ k Tki = T l¢ j¢ = Qj¢ l¢ ;Как видим, эта совокупность преобразуется по формулам (8) и, следовательно, является тензором. Тензор
Q с компонентами Qij= Tji называется тензором, сопряженным с тензором T. Будем использовать обозначение Q=T*.Тензор упругих напряжений
Широко используемым в механике сплошных сред тензором является тензор упругих напряжений. Рассмотрим упругое тело, деформированное внешними воздействиями. Мысленно вырежем в этом теле объем
V, ограниченный поверхностью SV.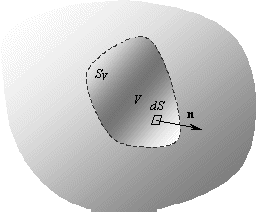
На каждый элемент
dS этой поверхности со стороны частиц тела, лежащих вне объема V, будет действовать сила, происходящая от деформации тела. Она, очевидно, пропорциональна площади dS этого элемента и зависит от ориентации площадки dS или, что по сути то же, от ориентации внешней относительно V нормали n к площадке. Обозначим эту силу через –pn dS. Появление здесь знака “минус” вызвано тем, что направление внешней нормали n составляет тупой угол с внешней силой, давящей на площадку dS объема V. Вектор pn представляет собой силу, отнесенную к единице площади. Он зависит от ориентации n и называется нормальным напряжением на площадку dS с нормалью n. В общем случае упругого тела направление этого вектора может лишь случайно оказаться параллельным нормали n.В каждой точке упругого тела каждому направлению
n отвечает свой вектор pn. Объем V мы можем вырезать (мысленно), например, так, чтобы нормаль n совпадала с ортом e1 или с ортом e2 или с ортом e3. Каждому направлению будет отвечать свой вектор pn. Покажем, что компоненты совокупности трех векторов pe1, pe2, и pe3 составляют тензор второй валентности.Обозначим через
f внешнюю силу, действующую на единицу массы тела (это может быть, например, сила тяжести), через r–плотность вещества, через a–ускорение объема dV. Согласно второму закону Ньютона равнодействующая сил, приложенных к объему dV, равна произведению его массы rdV на ускорение a.Пусть объем имеет форму достаточно малого тетраэдра, три грани из четырех которого параллельны координатным плоскостям, а четвертая перпендикулярна заданному направлению нормали
n.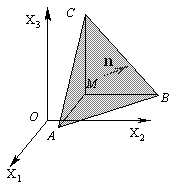
На грань
ABC, имеющую площадь S, будет действовать поверхностная сила, равная –pn S. На грань BCM, площадь которой S cos (n,^e1) равна проекции S на плоскость x1 = const, сила pe1 S cos(n,^e1). Исчезновение здесь знака “минус” здесь вызвано тем, что, как видно из рисунка, орт e1 имеет направление, противоположное внешней нормали к грани BCM. Аналогично на грани ACM и ABM действуют силы pe2 S cos(n,^e2) и pe3 S cos(n,^e3).Массовая сила, действующая на тетраэдр, имеющий объем
V, равна f r V. Применение второго закона Ньютона к объему V приводит к равенству–pn
S + pe1 S cos(n,^e1) + pe2 S cos(n,^e2) + pe3 S cos(n,^e3) + f r V = a r V,или
–pn
S + pe1 S cos(n,^e1) + pe2 Scos(n,^e2) + pe3 S cos(n,^e3) = (a – f) r V.Разделим это равенство на
S–pn + pe1 cos(n,^e1) + pe2 cos(n,^e2) + pe3 cos(n,^e3) = (a – f) r V / S.
и устремим длину ребер тетраэдра к нулю. При этом отношение объема тетраэдра к площади его грани
ABC также устремится к нулю, и мы получим–pn
+ pe1 cos(n,^e1) + pe2 cos(n,^e2) + pe3 cos(n,^e3) = 0,или
pn
= pe1 (n e1) + pe2 (n e2) + pe3 (n e3).Если в качестве нормали
n последовательно выбрать орты e1¢ e2¢ e3¢ другой прямолинейной прямоугольной системы координат, получим три соотношенияpe
1¢ = (e1¢ e1) pe1 + (e1¢ e2) pe2 + (e1¢ e3) pe3;pe2¢ = (e2¢ e1) pe1 + (e2¢ e2) pe2 + (e2¢ e3) pe3;
pe3¢ = (e3¢ e1) pe1 + (e3¢ e2) pe2 + (e3¢ e3) pe3,
или
|
pe k¢ = a k¢ i pei. | (11) |
Входящие в правые части векторы
pei могут быть записаны через компоненты следующим образом:pe1 =
s11 e1 + s12 e2 + s13 e3;pe2 = s21 e1 + s22 e2 + s23 e3;
pe3 = s31 e1 + s32 e2 + s33 e3,
или
|
pe i = sij ej. | (12) |
Аналогично представим и векторы
pej¢ через компоненты штрихованной системы координат:pe
1¢ = s1¢ 1¢ e1¢ + s1¢ 2¢ e2¢ + s1¢ 3¢ e3¢ ;pe2¢ = s2¢ 1¢ e1¢ + s2¢ 2¢ e2¢ + s2¢ 3¢ e3¢ ;
pe3¢ = s3¢ 1¢ e1¢ + s3¢ 2¢ e2¢ + s3¢ 3¢ e3¢ ,
или
|
pe k¢ = sk¢ l¢ el¢ . | (13) |
Величины
sij при переходе к другой прямолинейной прямоугольной системе координат преобразуются как компоненты тензора. Чтобы убедиться в этом, подставим соотношения (12) в формулу (11)pe
k¢ = a k¢ i sij ejи умножим левую и правую части этого равенства на
el¢ . С учетом формулы (13) получим:el¢ pek¢ =
т. е. совокупность величин
sij представляет собой компоненты тензора второй валентности.Симметричные и антисимметричные тензоры
ТензорSik, все компоненты которого удовлетворяют условию Sik=Ski, называется симметричным.
Из формулы (9) видно, что у симметричного тензора из девяти компонент независимыми являются только шесть, из которых три лежат на главной диагонали (
S11, S22, S33). Очевидно, что симметричный тензор является сопряженным самому себе.ТензорAik, все компоненты которого удовлетворяют условию Aik=–Aki, называется антисимметричным.
Диагональные элементы антисимметричного тензора равны нулю, так что независимы только три компоненты антисимметричного тензора из девяти. Тензор, сопряженный с антисимметричным тензором, отличается от последнего только знаком.
Свойство тензора быть симметричным или антисимметричным инвариантно, иными словами, сохраняется при переходе от одной прямолинейной прямоугольной системы координат к другой. Это ясно из определения тензора: если
Sik=Ski, тоSj¢ l¢
= a j¢ i a l¢ k Sik = a j¢ i a l¢ k Ski = a l¢ k a j¢ iSki = Sl¢ j¢ .Аналогично доказывается инвариантность свойства тензора быть антисимметричным.
Симметричный тензор может соответствующим выбором координатной системы быть приведенным к такому виду, когда недиагональные элементы равны нулю, как в формуле (6).
Тензор, у которого отличны от нуля только диагональные компоненты, называется приведенным к главным осям. Значения диагональных компонент, которые при этом получаются, называются главными значениями тензора.
Тензор второй валентности
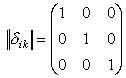
| (14) |
называется единичным тензором. При переходе от одной прямолинейной прямоугольной системы координат к другой он остается единичным:
|
d j¢ l¢ = a j¢ i a l¢ k dik = a j¢ k a l¢ k. | (15) |
Согласно формуле
(1.47) правая часть этого равенства дает d j¢ l¢ , так что мы имеем тождество.Тензоры, компоненты которых одинаковы во всех прямолинейных прямоугольных системах координат, называются инвариантными
Тензор произвольной валентности
Аналогично тензору второй валентности
определяется тензор произвольной валентности r:Если совокупность3r величин Tij…m при переходе от одной прямолинейной прямоугольной системы координат к другой преобразуется по формулам
| Tl¢ k¢ …n¢ = a l¢ i ak¢ j… an¢ m Tij…m, где ak¢ j=(ek¢ ej), | (16) |
совокупность этих3r величин Tij…m определяет геометрический объект, называемый тензором валентности r в трехмерном пространстве.
Согласно этому определению вектор является тензором валентности 1, а скаляр–тензором валентности 0.