

I. Векторы. 1.4. Произведение трех векторов
Из трех векторов можно составить произведения разного вида:
| (a×b)c; a(b×c); (a×c)b; |
| (a ´ b)×c; a×(b ´ c); (a ´ c)×b; |
| (a ´ b) ´ c; a ´ (b ´ c); (a ´ c) ´ b; |
Верхняя и нижняя строки дают векторы различных направлений, средняя – скаляры. Первая строчка дает очевидные результаты – скалярное произведение дает скаляр, и он умножается на вектор (или наоборот, вектор на скаляр).
Вторая строчка содержит векторно-скалярные, так называемые смешанные произведения трех векторов. Геометрическое значение первого во второй строчке смешанного произведения видно из рисунка: модуль векторного произведения дает площадь основания построенного на векторах параллелепипеда, модуль проекции вектора
c на это векторное произведение дает высоту параллелепипеда,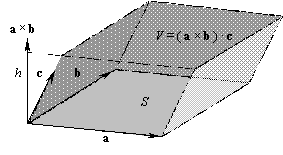
следовательно, модуль смешанного произведения равен объему этого параллелепипеда. Смешанное произведение положительно, если вектор
c составляет острый угол с векторным произведением, как на рисунке, в противном случае отрицательно. Очевидно (из рисунка),| (a ´ b)×c = (c ´ a)×b = (b ´c)×a. | (25) |
А т. к. a ´ b = -b ´ a, имеем также
| -(a ´ b) ×c = (b ´ a)×c = (a ´ c)×b = (c ´ b)×a. | (26) |
В компонентах смешанное произведение представляется определителем
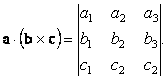
| (27) |
Рассмотрим теперь двойное векторное произведение. Вектор
a ´ (b ´ c) перпендикулярен вектору a и векторному произведению b ´ c, т. е. нормали к плоскости, содержащей эти два вектора. Следовательно, он компланарен этим векторам и может быть представлен в виде:| a ´ (b ´ c) = m b + n c. | (28) |
Найдем скалярные параметры
m и n. Умножим скалярно последнее равенство на вектор e1, лежащий в плоскости векторов b и c, перпендикулярный вектору c и направленный так, чтобы векторы e1, c и b ´ c образовали правую тройку векторов: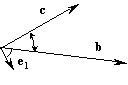
{a ´ (b ´ c)} e1 = m b
×e1 + n c×e1= m b×e1.В левой части равенства сделаем циклическую перестановку векторов
a, (b ´ c) и e1 в соответствии с формулой (25):{
(b ´ c) ´ e1} a = m b×e1.В фигурных скобках произведение взаимно перпендикулярных векторов, направленное по вектору
c. Длина вектора b ´ c равна b c sin (b,^c), а поскольку вектор e1 единичный, длина вектора (b ´ c) ´ e1 также равнаb c
sin (b,^c) = b c cos (b,^ e1) = c (b×e1).Учитывая направление этого вектора, можем записать
(b ´ c) ´ e1 = c ( b
×e1) c / c,{(b ´ c) ´ e1} a = ( b×e1) (a×c) = m b e1.
Сокращая левую и правую части на отличный от нуля скаляр
b×e1, получим| m = (a×c). | (29) |
Чтобы найти
n, перепишем формулу (28) в видеa ´
(c ´ b) = –m b – n c.Здесь переставлены векторы
b и c; воспользуемся только что полученным результатом: на основе формулы (29) сразу можем написать| – n = (a×b). | (30) |
Подставляя соотношения (29), (30) в формулу (28), находим
| a ´ (b ´ c) = b(a×c) – c(a×b). | (31) |
Обычно эту формулу называют формулой “бац минус цаб”, хотя следует помнить, что она может быть переписана и в следующих равноценных формах:
|
a ´ (b ´ c) = b (a×c) – (a×b) c;a ´ (b ´ c) = b (c×a) – c (a×b); a ´ (b ´ c) = b (c×a) – (b×a) c, |
(32) |
и т. д.
Используя двойное векторное произведение, можно произвольный вектор разложить на два, один из которых параллелен данному орту
e, а другой – перпендикулярен: полагая в формуле (31) a = c = e, получаемe ´
(b ´ e) = b (e×e) – e (e×b) = b – e (e×b),откуда
| b = e (e×b) + e ´ (b ´ e). | (33) |
Первое слагаемое параллельно орту
e, второе – перпендикулярно.