3. Основы векторного анализа

  1. 1.Векторы
  2. 2. Тензоры
  3. 3. Основы векторного анализа
  4. 3.1. Переменные векторы, зависящие от скалярного аргумента
  5. 3.2. Функции от векторгого аргумента
  6. 3.3. Поток вектора через поверхность. Дивергенция вектора. Формула Гаусса-Остроградского. Источники
  7. 3.4. Ротор вектора. Формула Стокса
  8. 3.5. Оператор Гамильтона
  9. Переменные векторы, зависящие от скалярного аргумента

    10. Годограф. Производная вектора по скалярному аргументу

    Если задан вектор a(t), изменяющийся вместе с переменной t, это эквивалентно заданию трех функций a1(t), a2(t) и a3(t) этой переменной, являющихся проекциями вектора a(t) на координатные оси. Для них определены, в частности, известные операции дифференцирования и интегрирования. С другой стороны, производная вектора a(t) может быть определена обычным образом как предел отношения

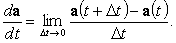
    Будем всегда предполагать, что a(t) – непрерывная векторная функция. Если под t понимается время, то в механике однократное дифференцирование по времени часто обозначают одной точкой над функцией:

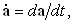
    вторую или третью производные по времени – соответственно двумя или тремя точками.

    Будем откладывать значения вектора a(t) при различных t от общего начала O. В результате изменения t в некотором интервале конец вектора a(t) опишет непрерывную кривую. Эта кривая называется годографом вектора a(t). Производная da/dt в каждой точке этой кривой направлена по касательной к ней.

    Представим вектор a(t) в виде a(t) = a(t)Чea(t), где ea(t) – орт и a(t) – длина вектора a(t). Тогда

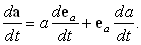
    (1)

    Если вектор a(t) меняется только по длине, не меняя своего направления, обращается в нуль первая производная правой части, и производная имеет направление самого вектора a(t). Годографом в этом случае служит прямая, проходящая через начало координат.

    Если остается неизменной длина вектора a(t), обращается в нуль второе слагаемое правой части формулы (1). Годографом будет кривая, лежащая на сфере радиуса a. Производная da/dt в каждой точке этой кривой будет направлена по касательной к ней, а следовательно, и к сфере. Поэтому da/dt перпендикулярна вектору a(t). Этот результат можно получить и другим способом. Поскольку в этом случае a2=a2=const,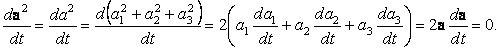

    Из равенства нулю скалярного произведения отличных от нуля векторов следует их взаимная перпендикулярность.

    Входящая в формулу (1) производная de/dt, как видно из рисунка, с учетом того что e – единичный вектор, равна

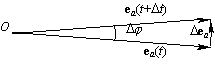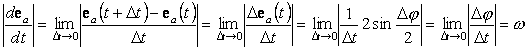
    (2)

    и, если t–время, представляет собой угловую скорость. С использованием вектора угловой скорости, перпендикулярного плоскости векторов ea(t + Dt) и ea(t), можем записать

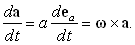
    (3)

    В общем случае, когда вектор a(t) меняется как по величине, так и по направлению, в формуле (1) первое слагаемое перпендикулярно вектору a(t), и его модуль может быть представлен в следующем виде:

    (4)

    Интегрирование функции скалярного аргумента

    Если

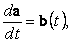
    то вектор a(t) называется неопределенным интегралом от вектора b:

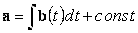
    Определенный интеграл

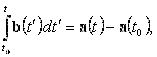
    равный разности значений вектора a(t) для границ интегрирования, можно рассматривать как предел интегральной суммы

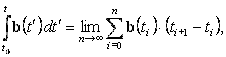
    (5)

    где ti–ряд значений аргумента t из интервала [t0,t] такой, что при n® ¥ наибольшая разность ti+1– ti стремится к нулю.

     

    Кривизна и кручение кривой

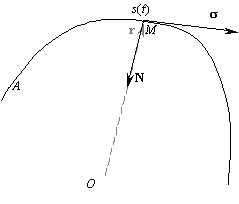
    Пусть точка M с радиус-вектором r описывает в пространстве некоторую кривую. Положение всякой точки M на этой кривой можно описывать не только радиус-вектором, но и длиной дуги s от некоторой заданной точки A на этой кривой. Тогда радиус-вектор r точки M можно представить как функцию скалярного аргумента s: r=r(s).

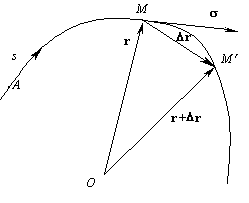    Выясним геометрическое значение первой и второй производных этой векторной функции. Рассматриваемая кривая является годографом радиус-вектора r, поэтому направление первой производной dr/ds совпадает с направлением касательной к кривой в сторону возрастания длины s дуги. Модуль же вектора dr/ds равен единице, т. к. длина дуги ds отличается от длины хорды | dr | на бесконечно малую второго порядка малости. Обозначим этот единичный касательный вектор (касательный орт) буквой s (сигма):

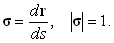
    (6)

    Его компонентами являются косинусы углов, образуемых им с координатными осями, равные

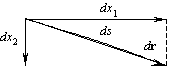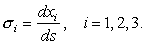
    (7)

    Сумма их квадратов равна |s|2=1:

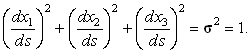
    (8)

    Рассмотрим теперь вторую производную радиус-вектора ds/ds=d2r/ds2. Поскольку s–единичный вектор, как и при выводе формулы (2) получим

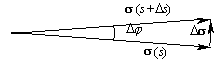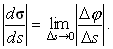
    (9)

    Вектор K=ds/ds перпендикулярен вектору s и называется кривизной кривой в данной точке. Величина, обратная модулю вектора K, R=1/|K|, называется радиусом кривизны кривой в рассматриваемой точке. В случае прямой линии вектор s не меняет своего направления, поэтому ds/ds=0, т. е. кривизна прямой линии равна нулю. Для окружности радиуса R по определению радианной меры угла имеем Ds=RDj, и кривизна ее по модулю равна 1/R.

    Проясним теперь вопрос о направлении вектора K. Пока нам известно лишь то, что он перпендикулярен вектору s.

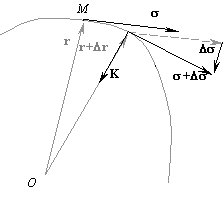    Плоскость, содержащая данную касательную и параллельная соседней бесконечно близкой касательной, называется соприкасающейся плоскостью.

    Вектор Ds лежит в соприкасающейся плоскости, т. к. векторы s, Ds и –(s + Ds) образуют треугольник. Поэтому и вектор кривизны K лежит в соприкасающейся плоскости. С другой стороны, вектор K перпендикулярен касательному к кривой в точке M вектору s.

    Плоскость, перпендикулярная касательной к кривой в точке M, называется нормальной плоскостью к кривой в точке M.

    Вектор K принадлежит, как видим, и нормальной плоскости.

    Прямые, лежащие в нормальной плоскости и проходящие через точку M, называются нормалями к кривой в этой точке. Та нормаль, которая лежит в соприкасающейся плоскости, называется главной нормалью.

    Таким образом, вектор кривизны K имеет величину

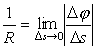
    (10)

    и направлен по главной нормали в сторону вогнутости кривой (к центру кривизны). Орт вектора кривизны обозначим буквой N. Тогда

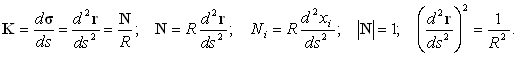
    (11)

    Последняя формула позволяет рассчитать радиус кривизны по известной r(s). В компонентах будем иметь

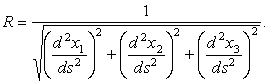
    (12)

    Та нормаль к кривой, которая перпендикулярна соприкасающейся плоскости, называется бинормалью.

    Бинормаль перпендикулярна ортам s и N. Введем третий орт b, |b|=1, направленный по бинормали в такую сторону, чтобы имело место соотношение

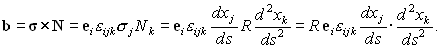
    (13)

    Изучение изменения направления касательного орта s привело нас к понятию кривизны кривой. Рассмотрение изменения ориентации соприкасающейся плоскости или, что то же, направления орта бинормали приводит к понятию кручения кривой. Т. к. b2=1, производная

    так что вектор db/ds перпендикулярен орту бинормали b. С другой стороны,

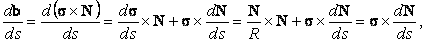
    (14)

    где использовано соотношение (11). Из последнего соотношения видно, что вектор db/ds перпендикулярен также касательному орту s. Следовательно, этот вектор параллелен оставшемуся из трех ортогональных ортов вектору N. Поэтому мы можем написать

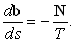
    (15)

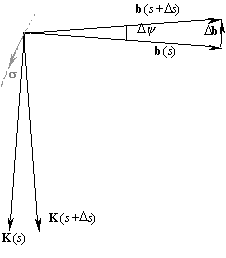
    Знак “минус” здесь поставлен для того, чтобы радиус кручения T был положительным для правого винта в правой системе координат (см. рис.) или левого винта в левой системе. Определяемая этим соотношением величина 1/T называется кручением кривой в точке M.

    Аналогично соотношениям (2) и (9) получаем

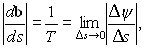
    (16)

    где Dy – угол между соседними бинормалями, отстоящими вдоль дуги на Ds. Если кривая плоская, то бинормаль не меняет своего направления, Dy = 0 и кручение равно нулю (радиус кручения – бесконечности). Следовательно, кручение является мерой отклонения рассматриваемой кривой от плоской кривой.

    Получим также формулу, описывающую изменение орта кривизны N. Для этого рассмотрим производную

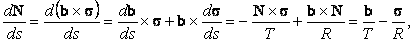
    (17)

    где использованы соотношения

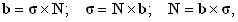
    (18)

    вытекающие из того факта, что орты b, s и N взаимно перпендикулярны и имеют такую же взаимную ориентацию, как орты координатной системы (независимо от того, является ли она правой или левой). Совокупность формул

    (19)

    носит название формул Френе.

    Рассмотрим вопрос о вычислении кручения. Из сравнения формул (14) и (15) находим

    циклическая перестановка векторов смешанного произведения приводит к формуле

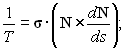
    (20)

    выражая далее орт касательной через производную s=dr/ds, а орт вектора кривизны через производную N=Rd2r/ds2, получаем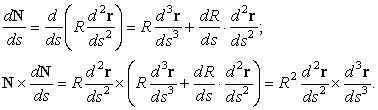

    Подставляя в формулу (20) для кручения, находим

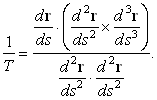
    (21)

    Эта формула показывает, что кручение T является псевдоскаляром, поскольку числитель представляет собой смешанное произведение–псевдоскаляр, а знаменатель–истинный скаляр.

     

    Кинематика материальной точки

    Рассмотрим движение материальной точки, заданное векторной функцией r = r(t). Годограф радиус-вектора r представляет собой траекторию точки. Скорость и ускорение точки определяются производными

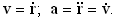
    Движение точки можно описать при известной форме траектории заданием пройденного к моменту времени t пути s для каждого t из определенного интервала. Тогда радиус-вектор можно представить сложной функцией времени t через посредство s, поэтому

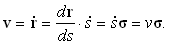
    (22)

    Последняя формула явно указывает, что вектор скорости направлен по касательной к траектории, а величина скорости

    равна производной пути по времени.

    Рассмотрим теперь ускорение материальной точки.

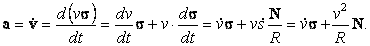
    (23)

    Здесь использована первая из формул Френе (19). Формула (23) представляет разложение ускорения на два слагаемых. Первое слагаемое, направленное по касательной к траектории, численно равно

    Второе слагаемое перпендикулярно траектории, направлено к центру кривизны по главной нормали и представляет собой нормальное (центростремительное) ускорение. Его величина равна v2/R. Величина полного ускорения равна

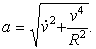
    (24)

    Если векторная функция r=r(t) задана своими компонентами, то

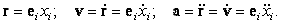
    (25)

    В п. 1.3 мы видели, что скорость любой точки твердого тела, вращающегося вокруг некоторой оси, может быть представлена формулой

    v = w ´ r

    		(26)

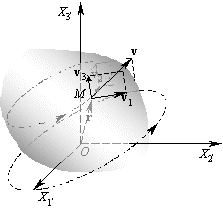
    где w – вектор угловой скорости, r – радиус-вектор этой точки, проведенный из начала отчета, лежащего на оси вращения тела.

    Докажем теперь, что если тело имеет неподвижную точку O, около которой оно вращается, то в каждый данный момент скорость любой точки M может быть выражена посредством формулы (26).

    Свяжем с твердым телом некоторую прямоугольную систему координат, имеющую начало в неподвижной точке. Тогда радиус-вектор фиксированной точки твердого тела, имеющей координаты в этой системе x1, x2 и x3, будет

    r=ei(t)xi

    		(27)

    Задать движение твердого тела можно различными способами. Например, можно представить орты жестко связанной с твердым телом координатной системы как заданные векторные функции времени. Каждый орт ei в неподвижной (штрихованной) системе координат определяется тремя компонентами e1¢ ei(t), e2¢ ei(t) и  e3¢ ei(t), i = 1,2,3, однако из девяти компонент ej¢ ei(t),  независимы лишь три, поскольку орты связаны шестью соотношениями

    eiek=dik

    		(28)

    Поэтому говорят, что имеющее неподвижную точку твердое тело обладает тремя степенями свободы. Таким образом, все компоненты ej¢ ei(t) могут быть выражены через некоторые три величины.

    Важно иметь в виду, что смысл формулы (27) существенно отличается от смысла первой из формул (25): там мы имели неподвижную систему координат, а функциями времени были xi(t); в формулах же (27) координаты xi от времени не зависят, тогда как функциями времени оказались ei(t).

    Производная радиус-вектора r фиксированной точки твердого тела по времени (скорость этой точки) равна

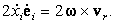
    (29)

    Ее проекции на координатные оси неподвижной штрихованной системы координат равны

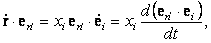
    а проекции на координатные оси вращающейся системы координат

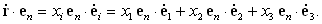
    (30)

    Имеют место соотношения

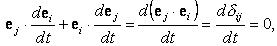
    откуда

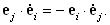
    (31)

    В частности, если i = j, правое равенство выполняется, только если скалярное произведение орта ei на производную от этого же орта по времени dei/dt равно нулю. Другими словами, орт ei перпендикулярен производной от него же по времени, если производная не равна нулю. Таким образом, из девяти произведений ejdei/dt можно составить антисимметричную матрицу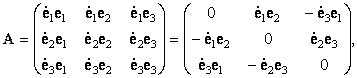

    которой, в свою очередь, можно поставить в соответствие некоторый псевдовектор w:

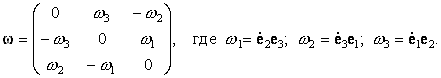
    (32)

    Тогда

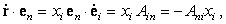
    и согласно формуле (II.50)

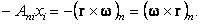
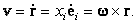
    (33)

    Формулами (32) определяются проекции вектора угловой скорости на оси вращающей системы координат. В неподвижной штрихованной системе

    ei=ej¢ a j¢ i

    		(34)

    с учетом этого формулы (32) можно представить в виде

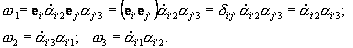
    (35)

    Общий случай движения твердого тела приводится к только что рассмотренному: если обозначить радиус-вектор начала O подвижной системы координат относительно начала координат O¢ неподвижной системы посредством r¢0, то

    r¢ =r¢0 + r = r¢0 + eixi;

    при дифференцировании по времени прибавится дополнительное слагаемое–производная от r¢0, представляющая собой скорость v¢0 точки O. Поэтому формула, дающая распределение скоростей различных точек твердого тела, примет вид

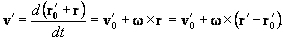
    (36)

    Для вычисления ускорения различных точек твердого тела дифференцируем скорость:

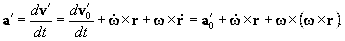
    (37)

    Таким образом, ускорение точек твердого тела состоит из трех частей–ускорения a¢0 точки O, вращательного ускорения

    и осестремительного ускорения

    Вектор последней составляющей перпендикулярен вектору угловой скорости и одновременно лежит в плоскости векторов w и r, что и дает основания называть его осестремительным ускорением.

     

    Дифференцирование вектора, отнесенного к подвижной системе координат

    Мы рассмотрели движение точки M, жестко связанной с движущейся (с вращением) системой координат. Пусть теперь точка M движется относительно подвижной системы координат. Если, как и ранее, обозначить радиус-вектор начала O подвижной системы координат относительно начала координат O¢ неподвижной системы посредством r¢0, то

    r¢=r¢0 + r=r¢0 + eixi

    от времени теперь зависят не только r¢0 и ei, но и xi, поэтому дифференцирование по времени дает скорость относительно неподвижной системы координат, которую назовем абсолютной скоростью, в виде

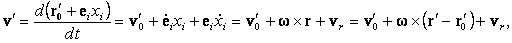
    (38)

    где последнее слагаемое представляет собой скорость точки M относительно подвижной системы координат – вектор относительной скорости точки M. Если бы координаты точки M были постоянными, скорость точки M относительно неподвижной системы координат была бы равной

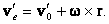
    (39)

    Эта часть скорости v¢ называется переносной скоростью движения точки M.

    Таким образом, вектор абсолютной скорости (скорости относительно неподвижной системы координат) равен сумме векторов переносной и относительной скорости:

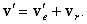
    (40)

    Если подвижная система координат только вращается относительно неподвижной, и их начала совпадают, то r¢0 = 0 и

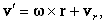
    (41)

    так что

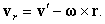
    (42)

    Рассмотрим теперь произвольный зависящий от t вектор a(t). Отложим его от начала O подвижной (вращающейся) системы координат. Предположим, что начала O и O¢ совпадают. Если рассматривать конец вектора a(t) как движущуюся точку, то относительную скорость конца вектора a(t) можно назвать относительной производной, применив для нее специальное обозначение

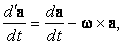
    (43)

    где использовано соотношение

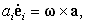
    (44)

    аналогичное соотношению (33).

    Рассмотрим теперь связь между абсолютным и относительным ускорением. Продифференцируем формулу (38):

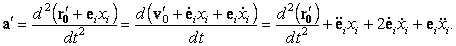
    (45)

    Если xi постоянны, последние два векторных слагаемых равны нулю, и оставшиеся два первых дают переносное ускорение

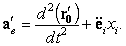
    (46)

    Для него можно использовать формулу (37)

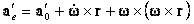
    (47)

    Последнее слагаемое формулы (45) представляет собой относительное ускорение:

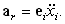
    (48)

    Предпоследнее слагаемое с учетом формулы (44), в которой вектор a заменим на вектор vr, представим в виде

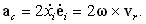
    (49)

    Эта часть абсолютного ускорения называется ускорением Кориолиса. Таким образом,

    Вектор абсолютного ускорения точки задается суммой трех векторов–вектора переносного ускорения, вектора ускорения Кориолиса и вектора относительного ускорения:

    a¢ =a¢ 0+ac+ar (50)